3. ステレオビジョンプログラムの配布
グラフカットを使用したステレオビジョンのプログラムを作りました. 共通のファイルとして scene1.row3.col1.ppmと scene1.row3.col3.ppmと makefileを使います. scene1.row3.col1.ppmとscene1.row3.col3.ppmは記事2で紹介したTSUKUBAステレオ画像の内の真値データに対応する左右2枚の画像です. GPUとCUDAを使う場合は以下のmakeのターゲットをdis_cからdis_gに,dep_cからdep_gに,3d_cから3d_gに変更してください. またこの記事で配布するプログラムはすべて自由に使ってもらって構いません (the MIT license).
Graph Cut Program for Stereo Vision
graph_cut.cppと graph_cut.cuが グラフカットプログラムの本体です.graph_cut.cppはCPUによるグラフカット, graph_cut.cuはGPUによるグラフカットになっています. どちらも3D Grid Graphに対してPush Relabel + Global Update方式でグラフカットを行っています. Global Update部分はCPUではキューによるアルゴリズムを使い, GPUではシェアードメモリによるアルゴリズムを使っています. これらは全く異なるアルゴリズムです.一方Push Relabel部分はCPUとGPUで同じアルゴリズムを使用しています.
グラフカットはグローバル変数の
- int SIZE_S;
- int SIZE_H;
- int SIZE_W;
- int SIZE_HW;
- int SIZE_SHW;
グラフカットの対象となる3D Grid Graphは次の図の様なステレオビジョン専用の10隣接枝グラフとなっています.
ただし図は奥行き方向Sと横方向Wだけが見える平面図で,縦方向Hは見えていません.
ソースノードSからシンクノードTへの方向を奥行き方向と言っています.
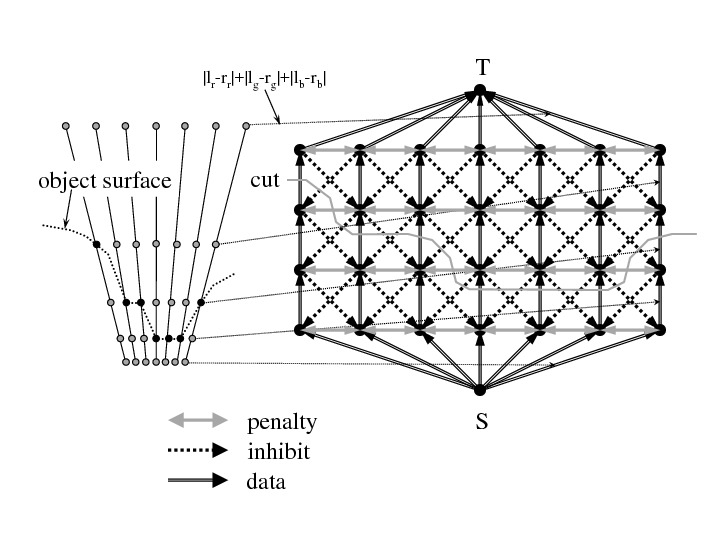
- 0: (reverse=9) (init_val=data_cost) front
- 1: (reverse=2) (init_val=penalty_h) up
- 2: (reverse=1) (init_val=penalty_h) down
- 3: (reverse=4) (init_val=penalty_w) left
- 4: (reverse=3) (init_val=penalty_w) right
- 5: (reverse=7) (init_val=zero) front right
- 6: (reverse=8) (init_val=zero) front left
- 7: (reverse=5) (init_val=inhibit_b) back left
- 8: (reverse=6) (init_val=inhibit_b) back right
- 9: (reverse=0) (init_val=inhibit_a) back
3D Grid Graphのサイズはグローバル変数の
- int SIZE_S;
- int SIZE_H;
- int SIZE_W;
記事2で紹介したTSUKUBAステレオベンチマークの真値視差画像では 最大視差(max_disparity)が28,最小視差(min_disparity)が10ですから, SIZE_S = max_disparity - min_disparity = 18とするとラベルは0から18までの19個となります. これが10から28に対応します.このようにSIZE_Sはその値そのものはノードの数なのですが, ラベルとして見るときは最大ラベルを表し,最小ラベルは0なので,ラベルの数はSIZE_S + 1となります. プログラムを作っているときはいつもこのことに気を付けていなければなりません.
Pixel-Disparith Model
disparity_stereo.cppは pixel-disparity modelによって視差画像ファイルを生成するプログラムです.
make dis_c
pixel-disparity modelであることは以下のcost()関数
int cost(int D, int H, int W) {
D += Min_depth;
int RR, RG, RB;
int LR, LG, LB;
int LW;
if (W+D > SIZE_W-1) LW = SIZE_W-1;
else LW = W+D;
call_rgb(rframe, H, W, &RR, &RG, &RB);
call_rgb(lframe, H, LW, &LR, &LG, &LB);
int d_R = (LR>RR)? LR-RR: RR-LR;
int d_G = (LG>RG)? LG-RG: RG-LG;
int d_B = (LB>RB)? LB-RB: RB-LB;
return d_R + d_G + d_B;
}実行は
./disparity_cpu right_image left_image max_disparity min_disparity penalty inhibit sacleGaze_line-Depth Model
depth_stereo.cppは gaze_line-depth modelによって視差画像ファイルを生成するプログラムです.
make dep_c
gaze_line-depth modelであることは以下のcost()関数
int cost(int D, int H, int W) {
D += Min_depth;
int RR, RG, RB;
int LR, LG, LB;
int RW;
int LW;
if ((W-D < 0) && (W+D > SIZE_W-1)) {
printf("Error\n");
}
else if (W-D < 0) {
RW = 0;
LW = 2*W;
}
else if (W+D > SIZE_W-1) {
LW = SIZE_W-1;
RW = SIZE_W-1-2*(SIZE_W-1-W);
}
else {
RW = W-D;
LW = W+D;
}
call_rgb(rframe, H, RW, &RR, &RG, &RB);
call_rgb(lframe, H, LW, &LR, &LG, &LB);
int d_R = (LR>RR)? LR-RR: RR-LR;
int d_G = (LG>RG)? LG-RG: RG-LG;
int d_B = (LB>RB)? LB-RB: RB-LB;
return d_R + d_G + d_B;
}実行は
./depth_cpu right_image left_image max_disparity min_disparity penalty inhibit magnification scale3D Stereo Vision Program
3d_stereo.cppは gaze_line-depth modelによるステレオビジョン処理の結果を3D表示するプログラムです.
make 3d_c| character | function |
|---|---|
| q | quit |
| ? | help |
| e | toggle figure mode |
| m | left picture |
| , | stereo picture (do graph_cut) |
| . | right picture |
| s | depth(disparity) to front |
| t | depth(disparity) to back |
| h | eye move left |
| j | eye move down |
| k | eye move up |
| l | eye move right |
| f | eye move far |
| n | eye move near |
| ! | decrease base line |
| @ | increase base line |
| # | decrease focal length |
| $ | ncrease focal length |
| % | decrease pixel size |
| ^ | increase pixel size |
| z | decrease penalty |
| x | increase penalty |
| Z | decrease inhibit |
| X | increase inhibit |
プログラムの起動は
./3d_cpu right_image left_image max_disparity min_disparity penalty inhibit magnification背景知識
ステレオマッチングは左右の画像の対応する点のずれ, すなわち視差,を検出して,この視差から対象の空間配置を推定する技術です. 視差から空間位置を推定するのは三角測量の計算をすれば良いだけですので, どうやって対応する点を見つけるかが問題の本質であると考えられてきました. ですので左右のステレオ画像から空間位置を推定する問題はステレオマッチングと呼ばれています. 教科書の章立てや項目名もステレオビジョンではなくてステレオマッチングとなっていることが普通です. 2つの画像から対応する点を見つける2D(画像)処理の後に,空間の配置を決定する3D処理を行う, すなわち別々の処理として扱ってきたということです. 対応を見つけようとするステレオマッチングという用語や視差という概念に縛られすぎてきた, ステレオビジョンを考え直して見ようというのがこのHPの趣旨ですが, しばらくはこれまでの考え方を説明します.
対応を見つけるために,特徴のある点(特徴点,コーナーと呼ばれる)の特徴量の類似性や配置の対応検出, 矩形領域の画像の類似性などが使われてきました. これらは
- Feature-based stereo matching
- Region-based stereo matching
- Pixel-based stereo matching
稠密ステレオでは,右画像の全てのピクセルに視差を割り当てる問題を解くことになります. 視差を割り当てるのがなぜ右画像なのかというと,右方向を正とすることが自然なので,視差を正とすると, 右画像のあるピクセルに投影された空間上の点は左画像では少し右のピクセルに投影されるのですから, 左画像でどれだけ右に現れるかを視差と呼んで, 「右画像のピクセルに右方向の視差,すなわち正の視差を割り当てる」のが自然というわけです.
右画像の全てのピクセルに視差を割り当てる様な問題はサイトラベリング問題と呼ばれます. サイトは場所のことで場所に何らかのラベルを割り当てる問題というわけです. 今の場合はピクセルが場所で,視差がラベルになります. 割り当ての数はラベル数のサイト数乗 \begin{align*} assign\_num=label\_num^{site\_num} \end{align*} という膨大な数となります. この中から1つの割り当てを選ぶ訳ですが,普通は割り当てに対して単一の数値を与える関数を定義して, その数値が最小となる割り当てを選択します. たった一つの数値で良いか悪いかを判断して良いのかと感じますが, これは物理学からのアナロジーで, エネルギーという単一の実数値を与える関数(その様な関数をハミルトニアンという)から その系のすべてが分かるという定式化を真似たものです. ですので,割り当てに与えられたこの単一の数値をエネルギー, エネルギーを与える関数をエネルギー関数, そして最小のものを選ぶことをエネルギー最小化と呼んでいます. そして割り当てを,物理的状態を表す用語である,配置と呼ぶこともあります.
サイトラベリング問題のエネルギー関数は\(f\)を割り当てとして \begin{align*} E(f)=E_{data}(f)+E_{smooth}(f) \end{align*} と表現されます.簡単のためサイトはピクセル,ラベルは視差として説明します. まず \(E_{data}(f)\) は画像データからピクセル毎に視差の割り当てが適切かどうかを決める項です. ピクセルだけを見て対応がはっきりと分かるようなステレオ画像であれば, この項だけで十分なのですが,実際は同じような明るさと色のピクセルばかりですから, ピクセル間の関係を見る第2の項 \(E_{smooth}(f)\) が必要になります.この第2項をどのようにするかは非常に重要な論点で様々なものが提案されています. まず隣接する2つのピクセルを問題にすることが最初の第一歩となります. たとえば視差は隣接するピクセル間で大抵はそんなに大きく変化しないだろうというものです. すなわち第2項はsmooth性に関するものだということで \(E_{smooth}\) という名前が使われます.
2つのサイトの関係を問題にする場合を1階と言い, 3つ以上のサイトの関係を問題にする場合を高階と言います. 1階であってもどのような関数にするかは大問題です. 特に視差は,大部分でスムーズに変化するものの, 対象の境界部分では大きく変化するのが当然ですから, 単にスムーズにするだけではいけない, 厄介なものだと考えられてきました. それで少しの変化では変化に応じてエネルギーを高くするものの, ある程度を超えるとそれ以上はエネルギーを大きくしない, 打ち切り比例 ( truncated linear ) と呼ばれる関数が良く使われています. なおある配置のエネルギーを高くするということはそのような配置を起こりにくくすることに対応します. 一方,gaze_line-depth modelでのdepthは, 視差のように対象の境界で大きく変化することがありませんので, 単純比例 ( linear ) の関数を使うことができます. 実は禁止条件があるのでdepthは隣接間で最大1しか変化しません. 禁止条件も入れて凸の関数にすることができます.
またエネルギーを最小にする配置を簡単に見つけられるかどうかはエネルギー関数の形に強く依存します. 1階のエネルギー関数が凸と言われる性質を持つときには, グラフカットを使って一気に最小配置を求めることができます. 打ち切り比例 ( truncated linear ) は凸ではないので, alpha expansionやalpha-beta swapなどの近似アルゴリズムが使われます.
この記事で紹介している最初のdisparity_stereo.cppは, pixel-disparity modelをlinearなエネルギー関数を使って一気に最小配置を求めています. このlinearなエネルギー関数とはサイト対に対して \(E_{smooth}(f)=penalty*|i-j|\) と表現されるものです.ここで \(i\)と\(j\)は隣接するpixelのdisparity値です.
2番目のdepth_stereo.cppと3番目の3d_stereo.cppは, gaze_line depth modelを凸なエネルギー関数を使って一気に最小配置を求めています. この凸なエネルギー関数とはサイト対に対して \begin{align*} E_{smooth}(f)=penalty*|i-j|+inhibit*(|i-j|-1)*T(|i-j|>1) \end{align*} と表現されるものです.ここで\(i\)と\(j\)は隣接するgaze_lineのdepth値です. \(T(bool)\)は\(bool\)が真のとき1,そうでないとき0となるデルタ関数です. この式を見ると分かるように,inhibitを大きくすると隣接するgaze_lineのdepth値は最大1しか変化しません. このinhibitが記事2で指摘したgaze_line-depth modelの重要な性質を実現している訳です. これにより大部分でスムーズに変化するものの, 対象の境界部分では大きく変化するという厄介な視差の性質を考慮する必要がなくなり, グラフカットによる完全な最小化が可能な凸のエネルギー関数を使えるようになったのです.