TSUKUBAステレオベンチマーク

TSUKUBAステレオベンチマークtsukuba.zipは コンピュータビジョンのベンチマークで有名な The Middlebury Computer Vision Pagesから ダウンロードすることができます．tsukuba.zipを展開すると，

• scene1.row3.col1.ppm
• scene1.row3.col2.ppm
• scene1.row3.col3.ppm
• scene1.row3.col4.ppm
• scene1.row3.col5.ppm
• truedisp.row3.col3.pgm

視差が定義されすぎている

橙色のスタンドライトは一番手前にあるのですが，真値視差画像のスタンドライトのすぐ右にも視差が定義されています． 右画像のスタンドライトのすぐ右には一番奥の本棚が見えていますが，この部分は左画像では隠れて見えません． 従って本来の視差は定義されないはずです． 真値視差画像は右画像での対象までの距離をレーザーで測定したものから作られたという噂なので， 確かにground-truthなのですが，視差としてはこれをそのまま使うわけにはいきません．

注視線と奥行き番号

そこで右ピクセルに視差を割り当てる (pixel-disparity model) のではなく， 注視線に奥行き番号を割り当てる (gazeline-depth model) ことを考えます． そうすることにより実空間での位置関係をより正しく認識することができ，隠れて見えない場合を排除することができます．

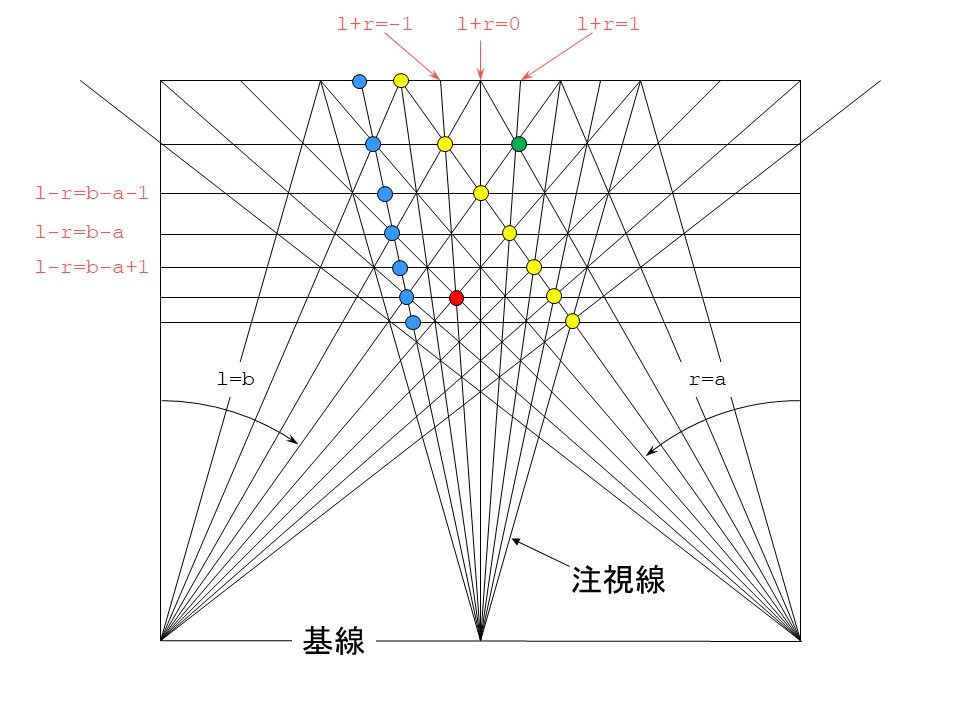
上の図でr, lはピクセル位置を表す整数の変数，aは負の整数定数, bは正の整数定数とします． r, lは画像の中心で0，かつ右方向が正の方向とします． r, lはそのピクセルを通過する左視線，右視線も表していることにします． l+r=整数定数となる左右視線の交点は，左右のカメラを結ぶ線分（これを基線 (base line) と言う）の中点から遠方に至る直線の上に乗ります． この直線を注視線 (gaze_line) と呼ぶことにします． またl-r=整数定数となる左右視線の交点は，base lineに並行な直線の上に乗ります． この直線に遠いほうから手前に向かって番号を振り，これを奥行き番号 (depth_number) と呼ぶことにします． 無限遠を0とすると，奥行き番号は視差と同じになります．黄色の〇はpixel-disparity modelを表しており， 青の〇はgaze_line-depth modelを表しています．

さてここで重要なことは， 注視線の数がピクセルの数の2倍になるということです． 同じピクセルで視差が1だけ異なると隣の注視線に移動しますが， 同じ視差でピクセルが1だけ異なると隣の隣の注視線に移動します． このことに注意すればpixel-disparity modelからgazeline-depth modelへの変換が可能です． なお，ピクセル数と同じ数の注視線を使う場合には奥行き方向の分解能が半分になります． プログラムではscale factorのことも考えておく必要があります．

次に赤の〇と緑の〇が真値視差から得られたとすると，この図から緑の〇は陰になって見えないことが分かります． 右画像の視差だけを考えていると気づかないのですが，左側も対等に考えると見えないことに気づきます． さらに注視線の位置変化に対して奥行き変化の方が大きいときは陰になるという関係があることが分かります． これは隣の注視線に移動するとき奥行きは最大で1しか変化しないということで非常に重要な性質です． 視差は隣接ピクセル間で大きく変化する可能性があるのに対し， 奥行きは隣接注視線間で最大1しか変化しないわけです． 記事3でinhibitという禁止のための値が出てきますが， これは奥行き (depth) の変化を隣接注視線間で最大1に抑えるためのものです．

修正後の視差画像

このようにして修正した視差画像(true.png)は次のようになります．視差が定義できないところ（オクルージョンと言う）は値が0となっており， 画像では黒くなっています．

プログラムの配布

この修正を行うプログラムtrue_disparity.cppは Ubuntu16.04LTS上で開発したものです． g++とOpenCV-3.0.0を使っていますが， OpenCVはimread()とimwrite()を使っているだけですのでバージョンは問わないと思います． コンパイルと実行はmakefileを使って

make

./true disparity_file_to_correct result_disparity_file scale_factor