11. Stereo Rectifier using Gaze_line-Depth Model
Z. Zhangのカメラキャリブレーション手法
良く知られているZ. Zhangの手法("A flexible new technique for camera calibration",
IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(11):1330-1334, 2000)では

試してみると満足できる結果を得るのはなかなか難しく, 記事5で紹介した安いUSBカメラ(ロジクールC270など)を2台使ったような場合には ステレオビジョンに使えるステレオ並行化精度は得られませんでした. ローリングシャッターであることや そもそもUSB接続が2本なので同時性はまったく無いも同然であることが 原因なのではと感じています. 数学的に矛盾を含むデータにアルゴリズムが弱いということだと思います. キャリブレーションボードを手に持ってカメラのキャリブレーションを行うなど言語道断であると 測量分野の研究者に言われたこともあります. しかし色々の角度で撮影しなくてはならないので何かに固定するのは簡単ではありません.
新しいカメラキャリブレーション手法
もっと頑丈な手法がないものかと考えていた時に,
Gaze_line-Depth Modelによるステレオビジョンのグラフカット値が
そのままステレオ並行化処理(Stereo Rectification)にも使えるのではと思いつき,
当時小栗研究室の4年生だった宮崎利全君の卒業研究のテーマに設定して,一緒に研究を進めました.
その時に宮崎君が撮影した写真を了解を得てこのページで使わせてもらっています.
3次元復元法(3D Reconstruction Method)と名付けたこの手法がどんなものかまず実行例をご覧ください.




つぎの実行例は左右で上下が大きくずれているのですが,ちゃんと並行化されます.




つぎの実行例は近くから遠くまで距離が連続的に変化して正対面がほとんど無いのですが,これもうまく行きます.




3次元復元法(3D Reconstruction Method)の原理
記事10で分かったことは左右のカメラ画像をうまく3次元回転させればステレオ並行化が達成できるということです. またZ. Zhangの手法ではこのステレオ並行化できる回転を演繹的な計算で求めています. そしてその計算と順序が矛盾を含むデータに弱いらしいということなので,できるだけ演繹的でない方法を考えてみます. そもそもグラフカットでエネルギーという評価値を最小にすることで3次元を復元しているということは, エネルギーが小さいほど3次元として尤もらしいということなので, カメラの配置も含めて3次元として尤もらしいかどうかもこのエネルギーで判定できると考えられます. そこで左カメラで3個,右カメラで3個ある回転の自由度に対し,任意の回転を行ってエネルギーの値が 小さくなるものを採用するという処理を繰り返し,それ以上エネルギーが小さくならなくなったら停止する というほんとうに基本的な手法を試したところこれがうまく行ってしまいました. 極小を脱出するような処理は全く必要ありませんでした.
上の実行例1に対してそれ以上エネルギーを小さくすることができなくなった回転の収束値の周りでエネルギーがどのように変化するかを調べてみると
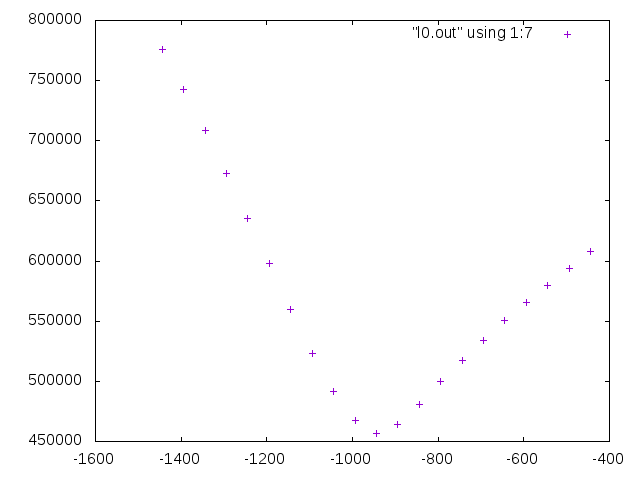
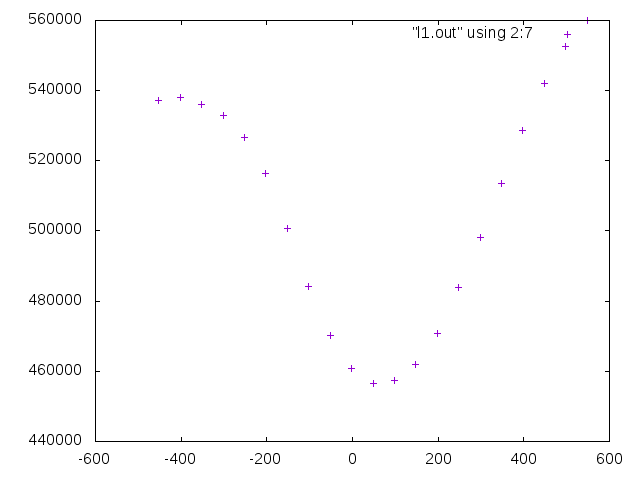
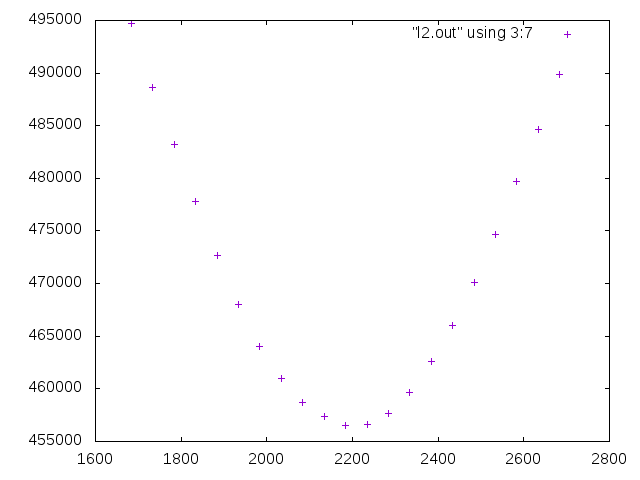
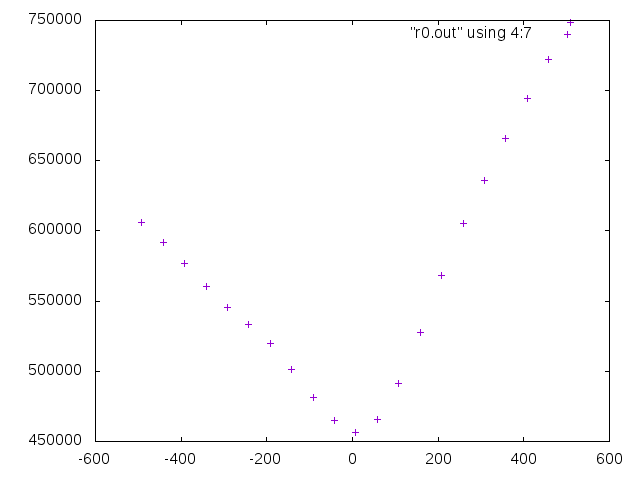
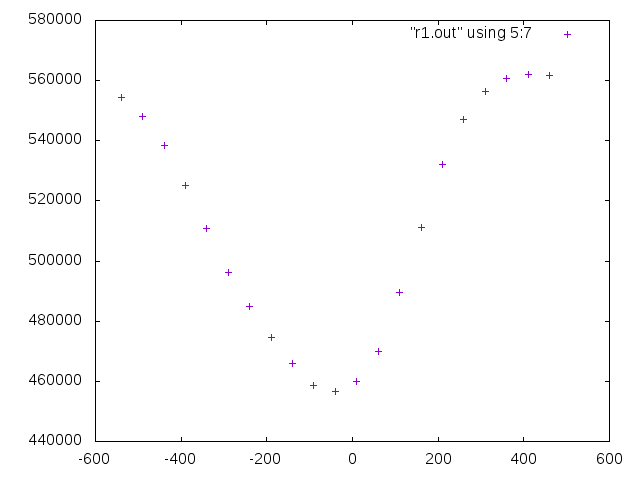
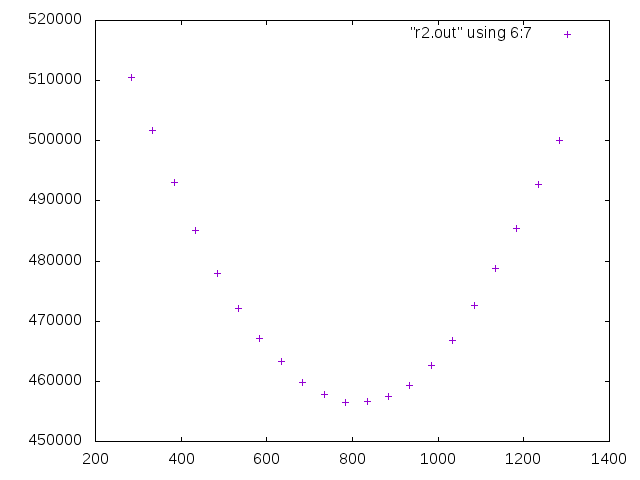
カメラ画像の3次元回転
カメラ画像の3次元回転そのものは記事10で説明したOpenCVのinitUndistortRectifyMap関数で行いますが, その前後は
void rotate(int l0, int l1, int l2, int r0, int r1, int r2) {
cv::Mat M = cv::Mat::zeros(3, 3, CV_64F);
M.at(0, 0) = focal/pixel;
M.at(0, 2) = double(XX-1)/2;
M.at(1, 1) = focal/pixel;
M.at(1, 2) = double(YY-1)/2;
M.at(2, 2) = 1.0;
cv::Mat D = cv::Mat::zeros(1, 5, CV_64F);
cv::Size S = cv::Size(XX, YY);
cv::Mat lV = cv::Mat::zeros(1, 3, CV_64F);
cv::Mat rV = cv::Mat::zeros(1, 3, CV_64F);
lV.at(0, 0) = 0.00001*l0;
lV.at(0, 1) = 0.00001*l1;
lV.at(0, 2) = 0.00001*l2;
rV.at(0, 0) = 0.00001*r0;
rV.at(0, 1) = 0.00001*r1;
rV.at(0, 2) = 0.00001*r2;
cv::Mat lR;
cv::Mat rR;
Rodrigues(lV, lR);
Rodrigues(rV, rR);
cv::Mat lmap1;
cv::Mat lmap2;
cv::Mat rmap1;
cv::Mat rmap2;
initUndistortRectifyMap(M, D, lR, M, S, CV_16SC2, lmap1, lmap2);
initUndistortRectifyMap(M, D, rR, M, S, CV_16SC2, rmap1, rmap2);
remap(lframe, llframe, lmap1, lmap2, cv::INTER_LINEAR);
remap(rframe, rrframe, rmap1, rmap2, cv::INTER_LINEAR);
} 3次元復元法(3D Reconstruction Method)の本体
3次元復元法(3D Reconstruction Method)の本体は
void calib(void) {
int l0 = 0; int l1 = 0; int l2 = 0;
int r0 = 0; int r1 = 0; int r2 = 0;
rotate(l0, l1, l2, r0, r1, r2);
int min = graph_cut();
for (int mul = 512; mul >= 8; mul /= 2) {
int flg = 0;
int step = 0;
for ( ; ; ) {
if (step == 0) l0+=mul; else if (step == 1) r0-=mul;
else if (step == 2) l0-=mul; else if (step == 3) r0+=mul;
else if (step == 4) l2+=mul; else if (step == 5) r2-=mul;
else if (step == 6) l2-=mul; else if (step == 7) r2+=mul;
else if (step == 8) l1+=mul; else if (step == 9) r1-=mul;
else if (step == 10) l1-=mul; else if (step == 11) r1+=mul;
else {}
rotate(l0, l1, l2, r0, r1, r2);
int now = graph_cut();
if (now >= min) {
if (step == 0) l0-=mul; else if (step == 1) r0+=mul;
else if (step == 2) l0+=mul; else if (step == 3) r0-=mul;
else if (step == 4) l2-=mul; else if (step == 5) r2+=mul;
else if (step == 6) l2+=mul; else if (step == 7) r2-=mul;
else if (step == 8) l1-=mul; else if (step == 9) r1+=mul;
else if (step == 10) l1+=mul; else if (step == 11) r1-=mul;
else {}
}
else {
flg = 1;
min = now;
}
step++;
if (step == 12) {
if (flg == 0) break;
flg = 0;
step = 0;
}
}
}
rotate(l0, l1, l2, r0, r1, r2);
}Z. Zhangの手法で焦点距離が分かる理由
次の2枚の写真はズーム機能が付いた,
すなわち焦点距離を変更できるカメラで撮影した同じキャリブレーションボードです.
どちらも同じだけ傾けて撮影し,どちらもキャリブレーションボードの右側が手前,左側が奥になっています.
また手前の右側は遠近で同じ大きさになるようにズームを調整しました.
この大きさをピクセルを単位とする長さの基準と考えることができます.
以下の長さや距離はすべてこの基準に対するものです.
円(楕円?)の上下の間隔と左右の間隔を見るとボードの傾きが分かり,
これから奥行きの距離(A)が分かります.これは2つの場合で同じになります.
一方奥に行くに従ってどれほど小さくなるかでカメラからの距離の比(B)が分かります.
実際の距離(A)と距離の比(B)からピクセルを単位とする焦点距離が求まることになります.


プログラムの配布
graph_cut.cu, rectify.cpp, makefile, 3_R.png, 3_L.pngをダウンロードしてください.
make do| character | function |
|---|---|
| q | quit |
| ? | help |
| M | do calibration |
| m | left picture |
| , | stereo picture |
| . | right picture |
| < | both picture |
| s | depth(disparity) to front |
| t | depth(disparity) to back |
| h | eye move left angle |
| j | eye move down angle |
| k | eye move up angle |
| l | eye move right angle |
| f | eye move near |
| n | eye move far |
| H | eye move left |
| J | eye move down |
| K | eye move up |
| L | eye move right |
| F | eye move forward |
| N | eye move back |
| C | clear angle and position |
./rec right_image left_image max_disparity min_disparity penalty inhibit divisor option